Splitting the Octave
A Graphical Model for Musical Scale Description and Creation
Keywords: scale, music education, music theory, information theory, graph theory, set theory, visualization.Edgar Matias, University of Toronto
James McGowan, North Texas State University
1993
Intro
Over the centuries, scales have played various roles in the universe of musical discourse. In addition to being the "stair-climbing" exercise of many a novice performer's daily regimen, they have also served as invisible scaffolding around which composers built melodies and harmonies. Indeed, 20th century composers started the practice of consciously building new scales to aid composition, a seemly logical approach which is nonetheless the reverse of historical precedent.
Despite their fundamental role, scales maintain an aura of inexplicability. Existing definitions range from broad ("a series of tones ascending or descending in pitch") to complicated (Agmon, 1989; Clough & Myerson, 1985). Broad definitions are ineffective information filters. Complicated definitions can be difficult to grasp. Experimentation and intuition are often easier routes to results.
In an effort at both order and simplicity, we present a simple graphical model of the musical scale.
Model Description
The ancient Greeks used the tetrachord as the basic unit for creating what we today would call a "scale". It consisted of four tones, the highest and lowest always separated by a perfect fourth. By varying the intervallic placement of the two middle tones, three types of tetrachords resulted: diatonic, chromatic, and enharmonic. Different scales can be created by using different combinations of these three basic tetrachords.
For example, we can form a traditional C major scale by combining two diatonic tetrachords separated by a tone. The lower tetrachord spans the notes C to F, followed by the separating tone, followed by the upper tetrachord spanning G to C.

Our model is analogous to that of the ancient Greeks, but rather than split the octave into tetrachords, we split it in half (into tritones).

Next, we position the two halves so that they lie parallel to each other. The result is a grid that increases by half tones (semitones) to the right, and by half octaves (tritones) upwards.

Note that we can also extend the grid beyond the length of an octave (shown below).
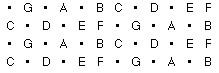
A scale is created by simply drawing horizontal and/or vertical lines onto the grid. In the language of graph theory, these lines are called "edges" and the notes they connect to are called "nodes". Each node represents a note in our newly created scale.
Below, we show the C major scale rendered using our model.
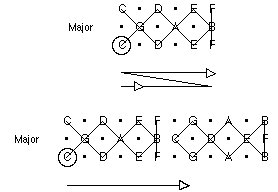
Other Scales Rendered
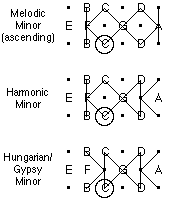
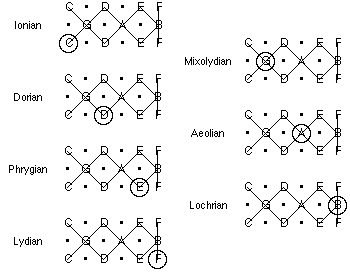
We have already shown how the C major scale is formed using our model. Below are other common scales, which we have rendered using this simple model.
Note also that it is quite easy to see similarities between different scales.
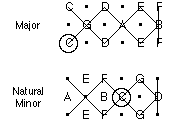
Pentatonic Scales
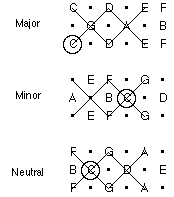

Medieval Modes
References
Agmon, Eytan (1989). A Mathematical Model of the Diatonic System. Journal of Music Theory, 29:249-270
Clough, John and Gerald Myerson (1985). Variety and Multiplicity in Diatonic Systems. Journal of Music Theory, 29: 249-270.
Copyright 1993 Edgar Matias & James McGowan